高考物理:《电磁感应》知识点及典型例题
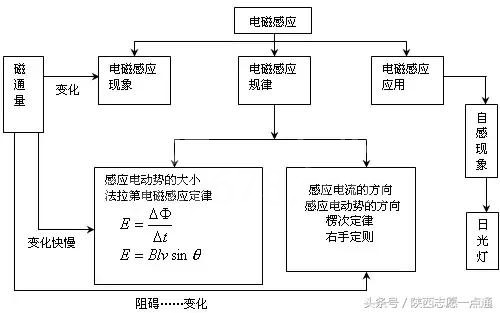
一、电磁感应现象
当穿过闭合回路的磁通量发生变化时,在闭合回路中产生感应电流的现象叫电磁感应现象.由
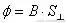
可知有三种情况可以使闭合电路中产生感应电流:
1. 闭合电路的一部分导体在磁场中做切割磁感线的运动,实际上此时闭合电路的面积发生变化,引起闭合回路中磁通量的变化;
2. 闭合电路所在处磁场的磁感应强度发生变化,引起闭合回路中磁通量变化;
3. 闭合电路垂直于磁感线的面积发生变化,引起闭合回路中的磁通量变化.
注意,若电路不闭合,则在电路两端产生感应电动势,而电路中没有感应电流.
二、法拉第电磁感应定律
感应电动势的大小跟穿过这一回路的磁通量的变化率成正比:
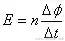
,这里注意区分磁通量、磁通量的变化量、磁通量的变化率。
公式
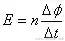
计算出来的是在
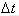
时间内的平均感应电动势,而瞬时感应电动势要取
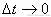
时的极限值.或用公式E=BLv来求。
三、楞次定律
1. 内容:
感应电流的磁场总是阻碍引起感应电流的磁通量的变化. 应用楞次定律实际上就是寻求电磁感应中的因果关系:因——穿过闭合电路的磁通量发生变化,果——产生感应电流,方法是由因求果.
2. 解决问题的步骤:
①弄清原磁场的方向以及原磁场磁通量的变化;
②判断感应电流的磁场方向:当磁通量增加时,感应电流的磁场与原磁场方向相反,当磁通量减小时,感应电流的磁场与原磁场方向相同;
③用安培定则判断出感应电流的方向.
3. 阻碍意义的推广:
(1)阻碍原磁场的变化。“阻碍”不是阻止,而是“延缓”,感应电流的磁场不会阻止原磁场的变化,只能使原磁场的变化被延缓,原磁场的变化趋势不会改变,不会发生逆转.
(2)阻碍的是原磁场的变化,如果原磁场不变化,即使它再强,也不会产生感应电流.
(3)阻碍不是相反.当原磁通减小时,感应电流的磁场与原磁场同向,以阻碍其减小;当磁体远离导体运动时,导体运动将和磁体运动同向,以阻碍其相对运动.
(4)“阻碍”的具体应用为:研究磁场的关系时遵循“增反减同”原则;研究相互作用力的效果时遵循“来拒去留”原则.
(5)由于“阻碍”,为了维持原磁场的变化,必须有外力克服这一“阻碍”而做功,导致其它形式的能转化为电能.因此楞次定律是能量转化和守恒定律在电磁感应中的体现.
4. 电势高低的判断
①分清内外电路:产生感应电动势的那部分导体为内电路,其余部分为外电路.
②判定电势的高低:在内电路中,感应电流从电源的负极流向电源的正极;在外电路中,感应电流从电源的正极流向负极.
四、自感现象
自感现象是指当线圈自身电流发生变化时,在线圈中引起的电磁感应现象,当线圈中的电流增加时,自感电流的方向与原电流方向相反;当线圈中电流减小时,自感电流的方向与原电流的方向相同.自感电动势的大小与电流的变化率成正比.
自感系数L由线圈自身的性质决定,与线圈的长短、粗细、匝数、有无铁芯有关.
自感电动势仅仅是减缓了原电流的变化,不会阻止原电流的变化或逆转原电流的变化.原电流最终还是要增加到稳定值或减小到零.
自感现象只有在通过电路的电流发生变化时才会产生.在判断电路性质时,一般分析方法是:当流过线圈L的电流突然增大瞬间,我们可以把L看成一个阻值很大的电阻;当流经L的电流突然减小的瞬间,我们可以把L看作一个电源,它提供一个跟原电流同向的电流.
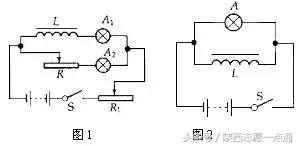
图2电路中,当S断开时,我们只看到A灯闪亮了一下后熄灭,那么S断开时图1电路中有没有自感电流?能否看到明显的自感现象,不仅仅取决于自感电动势的大小,还取决于电路的结构.在图2电路中,我们预先在电路设计时取线圈的阻值远小于灯A的阻值,使S断开前,并联电路中的电流IL>>IR ,S断开瞬间,虽然L中电流在减小,但这一电流全部流过A灯,仍比S断开前A灯的电流大得多,且延滞了一段时间,所以我们看到A灯闪亮一下后熄灭,对图1的电路,S断开瞬间也有自感电流,但它比断开前流过两灯的电流还小,就不会出现闪亮一下的现象.
五、电磁感应中的几类典型问题
例1、如图所示,有一个弹性的轻质金属圆环,放在光滑的水平桌面上,环中央插着一根条形磁铁.突然将条形磁铁迅速向上拔出,则此时金属圆环将( )
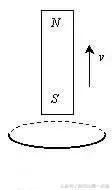
A. 圆环高度不变,但圆环缩小
B. 圆环高度不变,但圆环扩张
C. 圆环向上跳起,同时圆环缩小
D. 圆环向上跳起,同时圆环扩张
解析:在金属环中磁通量有变化,所以金属环中有感应电流产生,按照楞次定律解决问题的步骤一步一步进行分析,分析出感应电流的情况后再根据受力情况考虑其运动与形变的问题.
也可以根据感应电流的磁场总阻碍线圈和磁体间的相对运动来解答。当磁铁远离线圈时,线圈和磁体间的作用力为引力,由于金属圆环很轻,受的重力较小,因此所受合力方向向上,产生向上的加速度.同时由于线圈所在处磁场减弱,穿过线圈的磁通量减少,感应电流的磁场阻碍磁通量减少,故线圈有扩张的趋势。所以D选项正确。
<一>电磁感应中的力学问题
导体切割磁感线产生感应电动势的过程中,导体的运动与导体的受力情况紧密相连,所以,电磁感应现象往往跟力学问题联系在一起。
解决这类电磁感应中的力学问题,一方面要考虑电磁学中的有关规律,如安培力的计算公式、左右手定则、法拉第电磁感应定律、楞次定律等;另一方面还要考虑力学中的有关规律,如牛顿运动定律、动量定理、动能定理、动量守恒定律等。
例2、如图1所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L,M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下,导轨和金属杆的电阻可忽略。让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦。
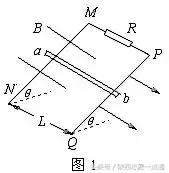
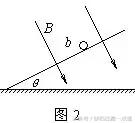
(1)由b向a方向看到的装置如图2所示,请在此图中画出ab杆下滑过程中某时刻的受力示意图;
(2)在加速下滑过程中,当ab杆的速度大小为v时,求此时ab杆中的电流及其加速度的大小;
(3)求在下滑过程中,ab杆可以达到的速度最大值。
解析:(18分)(1)如图所示:重力mg,竖直向下;
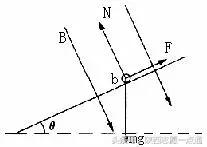
支撑力N,垂直斜面向上;
安培力F,沿斜面向上
(2)当ab杆速度为v时,感应电动势E=BLv,此时电路电流
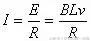
ab杆受到安培力
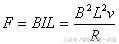
根据牛顿运动定律,有
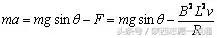
解得
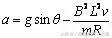
(3)当
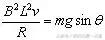
时,ab杆达到最大速度vm
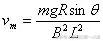
<二>电磁感应中的电路问题
在电磁感应现象中,切割磁感线的导体或磁通量发生变化的回路中将产生感应电动势将成为电源,将它们跟电阻、电容等构成回路即为电磁感应中的电路问题。
解决这类问题时,找准电源、正确判断电源的正负极是关键。
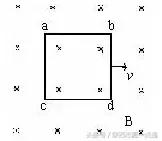
例3、如图所示,边长为l、总电阻为R的正方形线圈abcd处在磁感强度为B的匀强磁场中,线圈平面与磁场方向垂直,当线圈以速度v在垂直于磁场方向的平面内做匀速直线运动时,线圈中感应电流的强度I=__________,线圈回路中总的感应电动势E=________,a、c两点间电势差U=____________。
分析:只要导体做切割磁感线的相对运动,导体中就将形成感应电动势,该导体相当于一个感应电源;只要闭合回路的磁通量不变,无论回路中有几部分导体切割磁感线,无论回路中有几个感应电源,回路中的感应电流都为零。
解答:尽管线圈的ac和bd两边都做切割磁感线运动,但由于穿过线圈的磁通量不变,因此线圈中无感应电流,I=0;尽管线圈的ac和bd两边都切割磁感线运动,形成感应电动势均为Eac=Ebd=lvB的感应电源,但由于对整个线圈回路来说,Eac 和Ebd是反向串联的,因此线圈回路中的总的感应电动势为E =Eac-Ebd=0。由于线圈运动时,ac和bd两边相当于外电路开路的两个并联的感应电源,因此a、c两点间的电势差就等于两个并联感应电源的等次电动势,为U= E并=lvB。
例4、边长为a,总电阻为R的闭合正方形单匝线框,放在磁感应强度为B的匀强磁场中,磁感线与线框平面垂直.当线框由图示位置转过180°角的过程中,流过线框导线横截面的电量是多少?
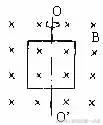
解析:一个平面有正、反两面,从正面穿入的磁通量设为正值,则从另一面穿入的磁通量就是负值、线框处于如上图所示位置时,磁感线从线框一面穿入,磁通量是Ф1=BS=Ba2,转过180°后磁感线从线框的另一面穿入,这时的磁通量就是Ф2=-BS=-Ba2,先后两次穿过线框磁通量的值相等,但正负不同,那么线框转180°过程中磁通量的变化量为
ΔФ=Ф2-Ф1=-Ba2-Ba2=-2Ba2。
取绝对值就是2Ba2.由此,可应用法拉第电磁感应定律求转180°过程中的平均感应电动势,最后应用欧姆定律和电流强度的定义式就可以求通过线框截面的电量.
设线框转180°所用时间为Δt,在这段时间内穿过线框的磁通量的变化量为ΔФ=2Ba2,根据法拉第电磁感应定律可得这一过程中平均感应电动势的大小为
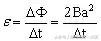
。
根据欧姆定律,Δt时间内线框中平均电流强度为
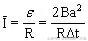
在Δt内流过线框导线横截面的电量
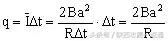
。
<三>电磁感应中的能量问题
产生感应电流的过程,就是能量转化的过程。
安培力对导体做正功,是将电能转化为机械能;安培力对导体做负功,是将机械能转化为电能。感应电流在电路中通过电阻又将电能转化为热能。
例5、如图3所示,宽L=0.5m的平行长金属导轨与水平面夹角θ=37°.与导轨平面垂直的匀强磁场磁感应强度B=1.0T.质量m=100g的金属棒ab垂直两导轨放置,其电阻r=1Ω,与导轨间滑动摩擦因数μ=0.25.两导轨由R=9Ω的电阻在下端相连.导轨及导轨与ab棒接触电阻不计(取sin37°=0.6,cos37°=0.8,g=10m/s2).求:
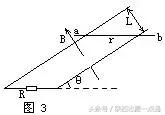
(1)当ab沿轨道向下运动,速度v=10m/s时,ab棒运动的加速度.
(2)ab棒沿轨道下滑的最大速度.
(3)ab棒以最大速度运动时,重力对ab棒做功的功率,ab棒产生的电功率以及输出的电功率.
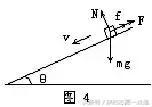
(1)ab棒在导轨上下滑时受力情况如图4所示,其中磁场力F=BIL=
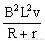
,摩擦力
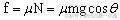
,根据牛顿第二定律,在沿轨道方向上
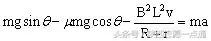
。
当v=10m/s时,ab棒运动的加速度大小是
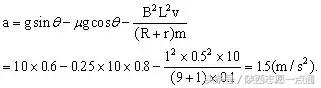
(2)当ab棒在导轨上运动加速度变为零时,开始做匀速运动,这时ab运动速度有最大值.由上述方程可知:mgsinθ-μmcosθ-B2L2v/(R+r)=0,
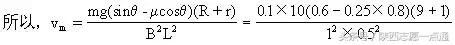
=16(m/s).
(3)重力做功的功率.P1=mgvsinθ=0.1×10×16×0.6=9.6(W).
金属棒ab产生的电功率
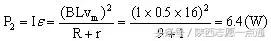
。
输出的电功率
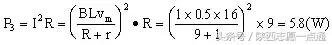
。
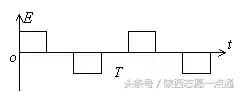
例6、如图xoy坐标系y轴左侧和右侧分别有垂直于纸面向外、向里的匀强磁场,磁感应强度均为B,一个围成四分之一圆形的导体环oab,其圆心在原点o,半径为R,开始时在第一象限。从t=0起绕o点以角速度ω逆时针匀速转动。试画出环内感应电动势E随时间t而变的函数图象(以顺时针电动势为正)。
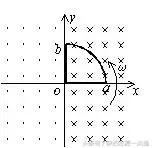
解析:开始的四分之一周期内,oa、ob中的感应电动势方向相同,大小应相加;第二个四分之一周期内穿过线圈的磁通量不变,因此感应电动势为零;第三个四分之一周期内感应电动势与第一个四分之一周期内大小相同而方向相反;第四个四分之一周期内感应电动势又为零。感应电动势的最大值为E=BR2ω,周期为T=2π/ω,图象如下。
今天的内容就先分享到这里,希望能够帮助到各位考生。更多学习方法、学习资料、学业测评、志愿填报等内容,可关注:陕西志愿一点通。
(来源:网络)
版权属于原作者或出版商所有,如涉及侵权请联系删除。
-
上一篇:高中物理一道力学习题的多种解法