高考物理：在利用气体状态方程解题时，..

在利用气体的状态方程解题时，每个方程的研究对象都是一定质量的理想气体，但是在有些问题中，气体的质量可能是变化的。那么，如何求解气体质量迁移问题呢？

一、恰当选取研究对象，将“变质量问题”转化为“定质量问题”

运用理想气体状态方程解决问题时，首先要选取一定质量的理想气体作为研究对象。对于状态发生变化过程中，气体质量发生变化的问题，如充气，漏气等，如何选择适当的研究对象，将成为解题的关键。

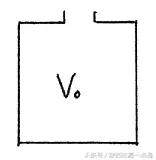
图1（a）

例1、如图1（a）所示，一容器有孔与外界相通，当温度由300K升高到400K对，容器中溢出的气体质量占原来的百分之几？

解法一：选取气体温度为300K时容器中的气体作为研究对象，当温度升高后，有一部分气体溢出，我们假设溢出的部分被一个“没有弹性可以自由扩张的气囊”装着，如图1（b）。

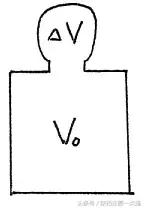
图1（b）

这样，当气体温度升高后，容器中的气体与“囊”中的气体质量之和便与初始状态相等。于是，将“变质量问题”转化成了“定质量问题”。由于本题压强未发生变化，状态参量列出如下：

初状态：

末状态：

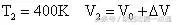
由盖吕萨克定律可知：

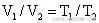
得

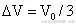
，则溢出的气体质量与原来总质量之比为：

。

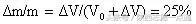
图1（c）

解法二：选取气体温度为400K时容器中剩余的气体作为研究对象。设所选对象在300K时的体积为

，如图1（c）示。以温度为300K时所选对象的状态为初状态，以温度为400K时所选对象的状态为末状态，则：

初状态：

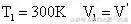
末状态：

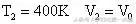
由盖吕·萨克定律可知：

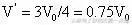
，说明最后剩余部分气体，在温度为300K时占总体积的75%，则溢出部分的气体占原来总质量的25%。

二、利用理想气体状态方程的推论，求解“变质量问题”

一定质量的理想气体（

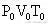
），若分成n个状态不同的部分

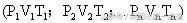
，则

。

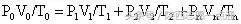
在利用此推论求解“变质量问题”时，要注意初状态的气体质量与末状态的各部分气体质量之和相等。

例2、潜水艇的贮气筒与水箱相连。当贮气筒中的空气压入水箱后，水箱便排出水，使潜水艇浮起。某潜水艇贮气筒的容积是

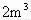
，贮有压强为

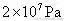
的压缩空气。一次，筒内一部分空气压入水箱后，压缩空气的压强变为

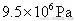
，求贮气筒排出的压强为

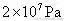
的压缩空气的体积。（假设在整个过程中气体的温度未发生变化）

解析：根据题意可知，一定质量的气体由初状态变化到末状态时，分成了2个状态不同的部分，即

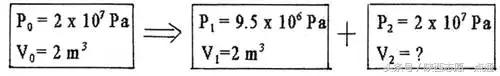
则：

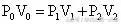
这样便可求出排出的压缩空气的体积

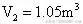
三、利用虚拟气体状态的方法求解“变质量问题”

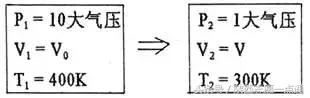
例3、容积一定的容器中盛有压强为10大气压，温度为400K的某种理想气体，用去30克气体并把温度降为300K时，压强变为7大气压。已知该气体在1大气压，300K时的密度为

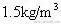
，求容器的容积和气体原来的质量。

解析：假设容器中原来的气体从状态1全部变为压强为1大气压，温度为300K的状态2，即

在状态2中取出用去的

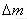
=30

克气体（这部分气体在状态2时所占体积为△V），而将剩余的气体作为状态

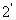
，并令其变为状态3。即

根据理想气体状态方程，则：

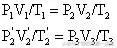
又因为

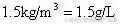
，所以

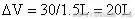
，这样便可求出容器的容积和气体原来的质量分别为

。

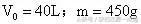
四、利用克拉珀龙方程（PV=nRT）求解“变质量问题”

例4、容积分别为9L，6L的A、B两容器，分别装有一定质量的同种理想气体，两容器用带阀门的细管相连，并分别置于300K和400K的恒温环境中，开始A、B中气压分别为10大气压和4大气压，打开阀门得重新平衡后，气体压强为多大？A中气体进入B中的部分占A中原有气体质量的百分之几?

解析：分别以A、B两部分气体作为研究对象，列出初末状态的参量如下：

初状态：

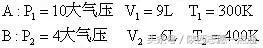
末状态：

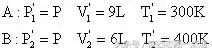
根据克拉珀龙方程，则：

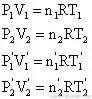
又因为初状态A、B两部分气体摩尔数之和等于末状态A、B两部分气体摩尔数之和，则有：

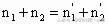
这样便很容易求出打开阀门重新平衡后气体的压强P＝8大气压，A中气体进入B中的部分与A中原有气体质量之比为：

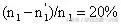
今天的内容就先分享到这里，希望能够帮助到各位考生。更多学习方法、学习资料、学业测评、志愿填报等内容，可关注：陕西志愿一点通。

（来源：网络）

版权属于原作者或出版商所有，如涉及侵权请联系删除。